optimization

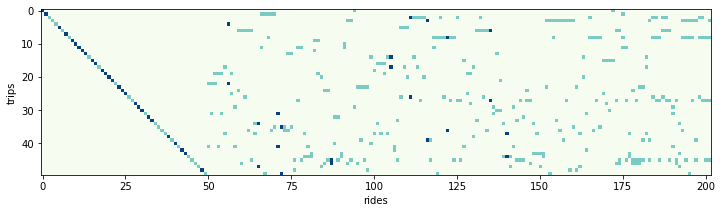
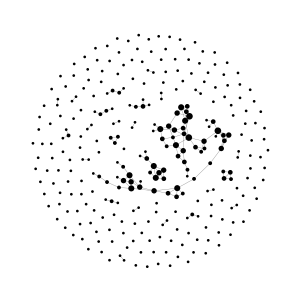
3000 travelers can form 1.55 x 10^16 rides shared by four of them. For the case of Amsterdam, only 130 of them are attractive and 44 are actually chosen in optimal solution. How to deal with the complexity, combinatorial explosion? See our efficient, behavioural algorithm applicable in realistic demand settings.

Research output in Transportation Research Part:B and on public github repo with Oded Cats

The premise of ride-sharing is that service providers can offer a discount, so that travellers are compensated for prolonged travel times and induced discomfort, while still increasing their revenues. While recently proposed real-time solutions support online operations, algorithms to perform strategic system-wide evaluations are crucially needed.

We propose an exact, replicable and demand-, rather than supply-driven algorithm for matching trips into shared rides. We leverage on delimiting our search for attractive shared rides only, which, coupled with a directed shareability multi-graph representation and efficient graph searches with predetermined node sequence, narrows the (otherwise exploding) search-space effectively enough to derive an exact solution. The proposed utility-based formulation paves the way for model integration in travel demand models, allowing for a cross-scenario sensitivity analysis, including pricing strategies and regulation policies. We apply the proposed algorithm in a series of experiments for the case of Amsterdam, where we perform a system-wide analysis of the ride-sharing performance in terms of both algorithm computations of shareability under alternative demand, network and service settings as well as behavioural parameters. In the case of Amsterdam, 3000 travellers offered a 30% discount form 1900 rides achieving an average occupancy of 1.67 and yielding a 30% vehicle-hours reduction at the cost of halving service provider revenues and a 17% increase in passenger-hours. Benchmarking against time-window constrained approaches reveals that our algorithm reduces the search-space more effectively, while yielding solutions that are substantially more attractive for travellers.